Mn II 4206 and 4326

The expected equivalent widths of Mn II 4206 and 4326 were calculated for each star, based on the mean Mn abundance derived from the other visible-region Mn II lines. For this calculation, we have made the usual assumption that the lines have only one component. The measured equivalent widths are compared to the calculated values in Table 4 (dilution effects in the binaries have been taken into account by scaling up the observed values). Fig. 3 demonstrates the discrepancy between the predicted strengths of both lines and their observed strengths, which tends to get worse at high abundances; stars with low abundances do not show this disagreement. From Fig. 4, it is clear that this discrepancy is more directly related to the strength of the lines than to the total atmospheric abundance of Mn.

Table 4: Mn II 4206 and 4326. The calculated values of are based on the assumption of single component line structures and are clearly too weak in stars with high Mn abundances. The individual line abundances are based on the adopted hfs multicomponent models in Table 5.

  
Figure 3: Mn II discrepancy in 4206 and 4326: calculated and observed equivalent widths are denoted by crosses and triangles respectively.

  
Figure 4: Mn II discrepancy in 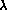4206 and 4326: ratio (obs/calc) versus equivalent width. The calculated values represent single-component line models. The points for the weakest Mn star have considerable uncertainty and are shown with appropriate large error bars.

Attempts to account for these anomalies by adjustments in atomic line parameters (, , ) or in stellar parameters () proved unfruitful. Further investigation revealed that the 4206 and 4326 features in the narrow-line star HR7775 (Figs. 5 and 6) were visibly broader than the other lines of Mn II . (Note that, for the work presented here, we did not make a detailed search for other Mn II lines with visible broadening or curve-of-growth anomalies, either of which could indicate strong hfs effects. A further search for lines which may show similar effects is the subject of future investigations.)

The most obvious candidate for a physical cause is hyperfine structure (hfs). We were unable to find any literature describing measured or theoretical hfs in these lines, but the behaviour observed in Figs 3, 4, 5, 6, 7 and 8 appears consistent with the hypothesis that their profiles are significantly affected by hfs: in weak-lined stars where the combined feature is too weak to be saturated, the hfs will effectively spread the lines out; in strong-lined stars where the feature is saturated, the action of the hfs will be to desaturate the lines, making them stronger.

This hypothesis was tested by constructing several simplified hfs models for these lines.

For 4206, each model contained a number of equal-strength components, spread over a wavelength range . The only constraint on was that the synthesized lines should be consistent with the width of the weak observed lines in HR 7775. We tested two- and three-component models (the total gf divided equally amongst the components) with the components spread over equal intervals. We found that splitting the line into three components (with = 0.086Å; see Table 5) allows the synthetic profile to fit well, at an abundance consistent with the other lines of Mn, for nearly all stars. Example plots of the way in which introducing hfs makes a fit to the 4206 line possible is shown for HR 7775 (Fig. 5) and HR 7361 (Fig. 7). The two-component model ( = 0.070Å) did not provide enough desaturation for the very strong-lined stars, nor did it fit HR 7775 at the line centre; we attribute lack of perfect agreement to the simplified symmetric structure adopted (normally hfs produces `flag' patterns, with a mixture of strong and weak components). Increasing the number of components beyond three had little further effect; once there is enough hfs to make the components individually unsaturated (separated from one another by 1 thermal line width) adding in extra components broadens the line wings but does not deepen it significantly. The actual pattern should have 15 components (, , ), so it is obvious that our model is only a crude approximation.

The 4326 line is visibly asymmetric in HR7775 and the other stars with low . After several trials, we adopted the simplified structure shown in Table 5 and Figs. 6 and 8 as a compromise, in order to avoid an overly complicated multiple-component model, while fitting reasonably well the asymmetric profiles in all the sharp-lined stars studied. Again, the actual (but unknown) hfs is undoubtedly very much more complicated, with 16 components (, ), some of which would be very weak. The approximation derived here permits reasonable-looking synthesis fits to all the stars in the sample.

Storey [1998] has made available preliminary calculations of the detailed hyperfine structure of 4206 of MnII especially for the present investigation. The uncertainties in the 15-component structure obtained are considerable and further work is needed. However, if we allow the derived pattern to have the largest width still consistent with our spectra of HR 7775 and HR 7361, the abundances derived (see Table 4) in the stars with the strongest lines would be reduced by a further 0.2 dex.

Without the hfs hypothesis, we can fit the 4206 and 4326 equivalent widths (in stars with strong Mn) only with an extremely high abundance (2-3 dex greater than that from the other lines of MnII ), and these synthetic profiles do not fit, as the line wings become too wide and the cores too shallow. Therefore, the hfs hypothesis solves the profile problem for both lines but does not completely eliminate the abundance discrepancy.

  
Table 5: Model hfs structures used for 4206 and 4326

The mean Mn II abundance (taken from the data in Table 2) is compared with the three-component results for 4206 in Table 4 and Fig. 9, and with the four-component results for 4326 in the same table and figure. As noted above, the trends in Fig. 9 show clearly that the simplified hfs models adopted here go a long way towards explaining the unexpected strengths of these lines, but do not entirely eliminate a discrepancy in derived abundance. The single exception to these trends is 33 Gem, which is treated in this work as a single star, but was suspected of being a double-lined spectroscopic binary by Hubrig & Launhardt [1993]. As previously noted, the question of binarity is not yet resolved, although our spectra did have the same `square' profiles observed by Hubrig & Launhardt.

Given the expectation that the hfs of these two lines should be very complicated, we believe that at least some of the residual trends of their abundance discrepancies vs. mean abundance from other lines may be due to the numerous weak hfs components. Our preliminary model using Storey's predictions does not predict complete elimination of the residual discrepancies although the effect is in the right direction. A laboratory study of the hfs in Mn II is urgently required to resolve these problems.

We also conducted an experiment to test the effect of systematic errors in microturbulence (see also the error discussion in Errors ): the results demonstrated that postulating substantially larger (1 kms) microturbulence in HR 7361, a star with very strong Mn II and a relatively low , has only a small (-0.1 dex) effect on the derived abundance.

  
Figure 5: The Mn II 4206 line in HR 7775 (histogram). A single line fit (dotted line) with the observed does not match well. Using a 2-component (dashed line) or 3-component (dot-dash line) hfs model (Table 5) provides increasingly better fits. Positions and relative strengths of components are shown by the marks below the line.

  
Figure 6: The Mn II 4326 line in HR 7775 (histogram). A single line fit (dotted line) for the observed does not match well. Using a 4-component (dot-dash line) hfs model (see Table 5) provides a better fit. Positions and relative strengths of components are shown by marks below the line.

  
Figure 7: The Mn II 4206 line in HR 7361 (histogram). A single line fit (dotted line) to the observed does not match well. Using the same hfs model as in Fig. 5 (dot-dash line) produces an improved fit.

  
Figure 8: The Mn II 4326 line in HR 7361 (histogram). A single line fit (dotted line) does not match well. Using the same hfs model as in Fig. 6 (dot-dash line) produces an improved fit.

  
Figure 9: The residual abundance excess from the simplified model hfs vs. mean Mn II abundance from the other visible-region lines. Filled squares, 4206; filled circles, 4326. Open symbols, 33Gem (see text).